學(xué)習(xí)數(shù)學(xué)的時(shí)候我們一定學(xué)習(xí)到一個(gè)遞歸公式，而在學(xué)習(xí)的過(guò)程當(dāng)中遞歸函數(shù)是非常簡(jiǎn)單的，但是如果想要用軟件來(lái)計(jì)算遞歸公式，該怎么做呢?接下來(lái)我們就一起來(lái)好好的了解一下吧。

　　遞歸函數(shù)詳解——遞歸函數(shù)簡(jiǎn)介

一種計(jì)算過(guò)程，如果其中每一步都要用到前一步或前幾步的結(jié)果，稱為遞歸的。用遞歸過(guò)程定義的函數(shù)，稱為遞歸函數(shù)，例如連加、連乘及階乘等。凡是遞歸的函數(shù)，都是可計(jì)算的，即能行的[1]。

古典遞歸函數(shù)，是一種定義在自然數(shù)集合上的函數(shù)，它的未知值往往要通過(guò)有限次運(yùn)算回歸到已知值來(lái)求出，故稱為“遞歸”。它是古典遞歸函數(shù)論的研究對(duì)象[1]。

遞歸函數(shù)介紹

在數(shù)理邏輯和計(jì)算機(jī)科學(xué)中，遞歸函數(shù)或μ-遞歸函數(shù)是一類從自然數(shù)到自然數(shù)的函數(shù)，它是在某種直覺(jué)意義上是”可計(jì)算的”。事實(shí)上，在可計(jì)算性理論中證明了遞歸函數(shù)精確的是圖靈機(jī)的可計(jì)算函數(shù)。遞歸函數(shù)有關(guān)于原始遞歸函數(shù)，并且它們的歸納定義(見下)建造在原始遞歸函數(shù)之上。但是，不是所有遞歸函數(shù)都是原始遞歸函數(shù)—最著名的這種函數(shù)是阿克曼函數(shù)。

其他等價(jià)的函數(shù)類是λ-遞歸函數(shù)和馬爾可夫算法可計(jì)算的函數(shù)。

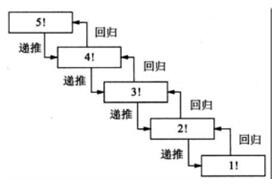
　　遞歸函數(shù)的案例

一個(gè)含直接或間接調(diào)用本函數(shù)語(yǔ)句的函數(shù)被稱之為遞歸函數(shù)，在上面的例子中能夠看出，它必須滿足以下兩個(gè)條件：

1)在每一次調(diào)用自己時(shí)，必須是(在某種意義上)更接近于解;

2)必須有一個(gè)終止處理或計(jì)算的準(zhǔn)則。

例如：

梵塔的遞歸函數(shù)

//C

voidhanoi(intn,charx,chary,charz)

{

if(n==1)

move(x,1,z);

else

{

hanoi(n-1,x,z,y);

move(x,n,z);

hanoi(n-1,y,x,z);

}

}

階乘的遞歸函數(shù)，公式如下：//C++

intFactorial(intn)

{

if(n==0||n==1)

return1;

else

returnn*Factorial(n-1)

}

以上就是有關(guān)遞歸函數(shù)的所有內(nèi)容，遞歸函數(shù)是數(shù)理邏輯和計(jì)算機(jī)科學(xué)當(dāng)中比較重要的一個(gè)函數(shù)公式，如果從事這方面內(nèi)容的朋友就不得不好好的學(xué)一學(xué)這一個(gè)函數(shù)的相關(guān)操作和技巧了，如果你還想了解更多與之有關(guān)的內(nèi)容，歡迎關(guān)注我們文軍營(yíng)銷的官網(wǎng)。

推薦閱讀

遞歸調(diào)用 遞歸調(diào)用如何使用 | 文軍營(yíng)銷遞歸調(diào)用就是在當(dāng)前的函數(shù)中調(diào)用當(dāng)前的函數(shù)并傳給相應(yīng)的參數(shù),這是一個(gè)動(dòng)作,這一動(dòng)作是層層進(jìn)行的,直到滿足一般情況的的時(shí)候,才停止遞歸調(diào)用,開始從最后一個(gè)遞歸調(diào)用返回。 fun(形參){ fun(參數(shù)值1)//第一次遞歸調(diào)用 fun(參數(shù)值2)//第二次遞歸調(diào)用 遞歸調(diào)用的使用方法 C語(yǔ)言中的遞歸 計(jì)算階乘的代碼 longfact...